Category: Numeracy Tasks

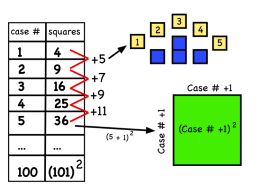
This is a great rich task to introduce the idea of patterning and algebra. This comes from Jo Boaler’s YouCubed site. She suggests to lead this activity as follows:

1. Ask “How do you see the shapes growing?” (Looking at shape and number)
2. Record variety of responses on chart paper. Then ask students to use their method to determine the number in the 100th case. What would it look like? How do the numbers relate to the visual solution?

3. Ask students to make a table of the results. Ask students to
use both the number pattern they see in their table and their visuals to
predict how many squares there would be in the 4th and 5th case. Even
though they have already thought about the hundredth case adding
more rows to their table can help them see the functional growth in both
the numbers and the shape. Keep encouraging students to connect the
numbers and visuals. Ask them where they see the extra squares in their
pictures and in the numbers in the table they have made.

4. Could you tell me how many squares there would be in any case, if I just told you the case number? Eg if I told you it was case 500 how many squares would there be? Write a sentence to describe how many squares there would be with any case number. This can lead to asking students to use a variable instead of the words.

Access this task and the handouts to go with it on the YouCubed site here.

Here is a great numeracy task from Peter Liljedahl’s website.

Adam, Bob, Clair and Dave are out walking: They come to rickety old wooden bridge. The bridge is weak and only able to carry the weight of two of them at a time. Because they are in a rush and the light is fading they must cross in the minimum time possible and must carry a torch (flashlight,) on each crossing.
They only have one torch and it can’t be thrown. Because of their different fitness levels and some minor injuries they can all cross at different speeds. Adam can cross in 1 minute, Bob in 2 minutes, Clair in 5 minutes and Dave in 10 minutes.
Adam, the brains of the group thinks for a moment and declares that the crossing can be completed in 17 minutes. There is no trick. How is this done? [from Nigel Coldwell]

 

Here is a solution to this task (found on Nigel Coldwell’s site):